Wavelets Extension Pack
Add powerful families of wavelet functions to your Mathcad Professional function library. Apply sophisticated wavelets techniques to your signal and image analysis and get greater accuracy and clarity in results.
The Wavelets Extension Pack CD lets you take a new approach to signal and image analysis, time series analysis, statistical signal estimation, data compression analysis and special numerical methods. Create an almost limitless number of functions that duplicate any natural or abstract environment. Functionality includes one- and two-dimensional wavelets, discrete wavelet transforms, multi-resolution analysis and more.
- Wavelet analysis results in greater accuracy and clarity. New wavelets field offers more sophisticated methods than those used conventionally, such as FFTs. View and explore details in data or signals that other techniques miss, destroy, or lose.
- Extensive functionality supports basic and advanced applications. The Wavelets Extension Pack integrates over 60 key wavelets functions, rivaling similar tools by MATLAB and Mathematica - at a more affordable price. Extensive coverage includes Orthogonal and Biorthogonal wavelet families including Haar, Daubelts, Symmlets, Coiflets and Bspline.
- Popular Mathcad interface provides best ease-of-use and fast application. Mathcad’s versatile environment is ideal for wavelets experimentation and performance of what-if scenarios. Plus, Wavelets Extension Pack’s superior integration with Mathcad and other add-on tools (including Signal Processing and Image Processing Extension Packs) gives you more power than ever. Also get extensive interactive documentation on wavelet fundamentals, applications, examples and reference tables.
System Requirements:
Mathcad 8 Professional or higher. At least 7 MB free hard disk space. CD-ROM drive.
Here the orthonormal wavelet transform is used to synthesize fractional Brownian motion (fBm). The theoretical underpinnings are developed in a paper of P. Flandrin (1992). A function is defined to create the approximate fBm from white noise in the wavelet transform domain by scaling the noise deviates at the level i by (2^I)^(H+1/2) times the standard deviation. With the appropriate fBm in the wavelet transform, you can get the representation in the time domain by simply performing the inverse wavelet transform.
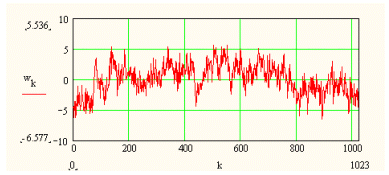
Due to the periodic nature of the wavelet transform, the above result is not a very good approximation to fBm. For example, the end points of the series are quite close to each other, which will not usually be the case for correctly simulated fBm series. To obtain a better approximation, you can generate a series of length and then subsample any len consecutive values in Mathcad using the Wavelets Extension Pack, in three steps.

The first difference of an fBm series is known as fractional Gaussian noise.

Note that, when the Hurst coefficient (the fBm scaling parameter) is equal to 1/2, a fractional Brownian motion becomes ordinary Brownian motion. You can obtain a simulation of samples of a Brownian motion by constructing a random walk process.

For comparison, here is what you get if you use the wavelet based approximate method with H=1/2

The power spectrum should have a slope close to -2 when plotted on a log-log scale.

The power spectrum of the first differences should have a slope close to 0 when plotted on a log-log scale.

Now extend the synthesis to create a 2-dimensional (2D) fractional Brownian Surface.

Again, the periodic nature of the wavelet transform forces the boundaries to match up closely, and a more accurate simulation can be obtained by generating a 4*len surface and then subsampling a len-by-len surface.

Selected Bibliography:
Bruce, Andrew and Gao, Hong-Ye. Applied Wavelet Analysis with S-PLUS. Springer-Verlag, New York, (1996) ISBN: 0-387-94714-0.
Cohen, A., Daubechies, I., and Vial, P. 'Wavelets on the interval and fast wavelet transforms.' Applied and Computational Harmonic Analysis, 1,54-81 (1993).
Daubechies, I. Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics, Philadelphia, PA (1992).
Donoho, David. L. and Johnstone, Iain M. 'Ideal Spatial Adaptation via Wavelet Shrinkage.' Biometrika, 81:425-455 (1994).
Harr, A. 'Zur theorie der othogonalem Funktionensysteme.' Mathematsche Annalen, 69, 331-371 (1910).
Hubbard, Barbara Burke. The World According to Wavelets : The Story of a Mathematical Technique in the Making. A K Peters Ltd., Wellesley, Massachusetts (1997). ISBN: 1-56881-047-4
Rao, K. R. and Yip, P. Discrete Cosine Transform: Algorithms, Advantages, Applications. Academic Press, Inc. Boston (1990) ISBN : 0-12580-203-X
Wornell, G. W. Signal Processing with Fractals: A Wavelet-Based Approach. Prentice Hall (1996).